Wi-Fi是为数不多让我能感到工作技能与生活产生交集的领域,毕竟不是每个人都有自己的网站,但几乎每个人家里都会有Wi-Fi。
成为黑客的第一步,就是破解Wi-Fi密码。——亚历山大·伊万诺维奇·斯米尔诺夫(Alexander Ivanovich Smirnov)
WEP,中文名称为有线等效加密,是第一个被广泛采用的Wi-Fi安全协议,首次出现于1997年 通过的 IEEE 802.11 标准。如今想找到一个支持WEP的设备以及不容易了。
WEP设计的安全性体现在以下三点:
消息机密性
无线网络的安全性最基本的就是要能够防止故意窃听,WEP使用RC4算法对无线数据进行加密,使得数据在无线网络中传输时不被窃听。
接入控制
在合法用户之间提供接入控制,来防止其他用户任意接入无线信道而影响合法用户。每个想要接入信道的合法用户都需要提供正确的共享密钥,这也有效地降低了非法用户的恶意攻击。
消息完整性
为了保证数据在无线网络传递过程中的完整性,WEP提供CRC32算法进行完整性校验,通过验证校验值确定传输的消息是否被篡改。
WEP 协议由认证协议和加密协议两个部分组成。其中认证协议用于确认通信双方的身份,加密协议用来确保通信数据的秘密性。而正是WEP的加密协议存在的缺陷,使得破解WEP密钥成为可能。
WEP加密协议原理
下面是WEP的加密协议的流程图
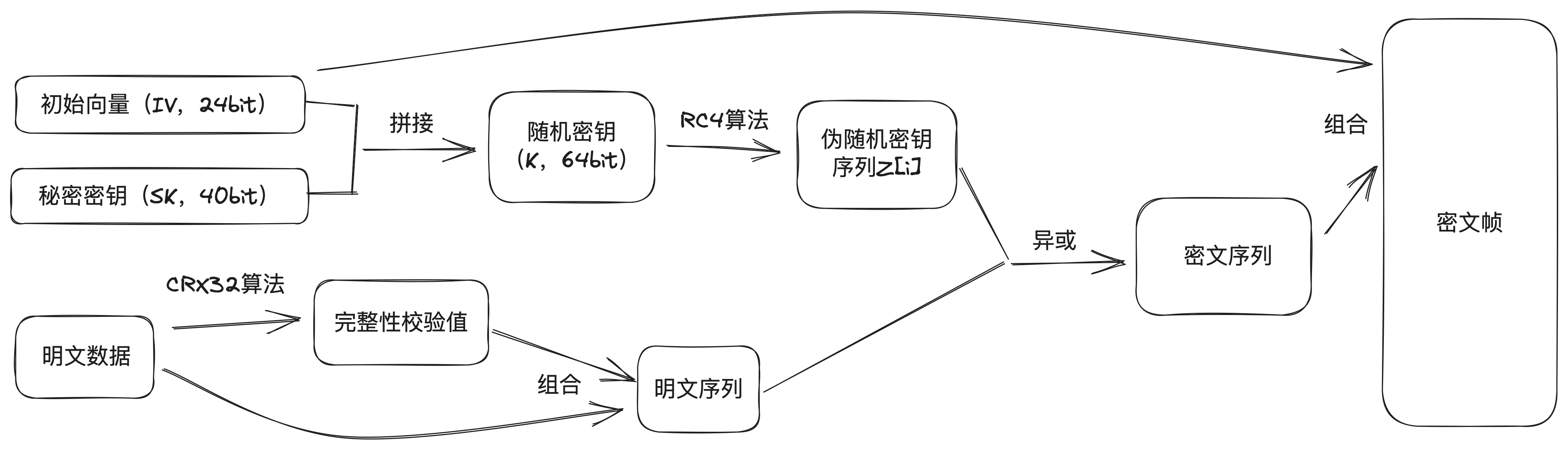
总体流程可以归纳为:
把用户输入的秘密密钥(SK,40bit)和初始向量(IV,24bit)拼接成随机密钥(K,64bit)
把随机密钥经由RC4算法生成伪随机密钥序列
把明文数据经过CRC32算法加密,再与它本身组合生成明文序列
用明文序列和伪随机密钥序列的异或结果作为密文序列
将初始向量和密文序列合成密文帧
其中,初始向量为随机生成,秘密密钥则是我们常说的Wi-Fi密码。
从流程图中不难看出,初始向量为明文传输。
RC4算法
RC4是一种串流加密算法,密钥长度可变。它加解密使用相同的密钥,因此也属于对称加密算法。它由两部分组成:密钥调度算法KSA(KeyScheduling Algorithm)和伪随机密钥序列生成算法PRGA(Pseudo Random Generation Algorithm)。
密钥调度算法KSA将输入L字节的随机密钥K生成一个由N个元素组成的排列 $S$,L一般为8或16,N一般为256。
以下是KSA的python实现:
def KSA(key):
S = list(range(256)) # 初始化S盒为0到255的列表
keyLength = len(key)
j = 0
for i in range(256):
j = (j + S[i] + key[i % keyLength]) % 256
S[i], S[j] = S[j], S[i] # 交换S[i]和S[j]的值
return S
# 示例密钥为64位的二进制数
key = [0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0]
# 调用函数进行密钥排列初始化
S_box = KSA(key)
print(S_box) # 输出排列后的S盒
伪随机密钥序列生成算法PRGA将两个索引 $i$ 和 $j$ 初始化为0,然后循环执行四个简单的操作:
递增 $i$ 作为计数器,伪随机递增 $j$ ,交换索引 $i$ 和 $j$ 指向的 $S$ 中的两个值,以及输出 $S[i] + S[j]$ 指向的值。需要注意的是,在任何连续的N轮中, $S$ 的每个元素至少会被交换一次(可能是与自身交换),因此在输出生成过程中, $S$ 的排列会相当快速地演变。
以下是PRGA的python实现:
def PRGA(S, n):
# 生成密钥序列
key_stream = []
i = 0
j = 0
for _ in range(n):
i = (i + 1) % 256
j = (j + S[i]) % 256
S[i], S[j] = S[j], S[i] # 交换元素
k = S[(S[i] + S[j]) % 256] # 生成密钥
key_stream.append(k)
return key_stream
FMS攻击
然而,RC4算法在某些特定情况下,由于密钥调度算法KSA的设计特性,导致输出的第一个伪随机密钥字节有5%的概率与输入的某些特定元素相关联。
记密钥调度算法KSA中循环进行 $i$ 次后随机排列 $S$ 的状态为 $S_i(i = -1,0,1,…,N-1) $,$S_{-1}$ 表示第一次循环之前排列 $S$ 的状态。具体地说,假设在第 $i$ 次循环中,令
$$ X=S_i[1] $$
$$ Y=S_i[X]=S_i[S_i[1]] $$
$$ Z=S_i[X+Y]=S_i[S_i[1]+S_i[S_i[1]]] $$
其中 $S_i$ 表示第 $i$ 次循环后的状态向量 $S$ 。在理想情况下,每次循环中元素的交换应该是随机的,没有特定的概率分布。然而,研究发现,约有5%的概率存在这样一种情况:在第 $i$ 次循环后,$X$、$Y$和$Z$都没有参与交换操作,它们的值保持不变。在这种情况下,我们就有
$$ Z=S_i[X+Y] $$
此时的 $Z$ 为RC4算法输出的第一个伪随机密钥字节。
再把目光转回随机密钥$K$,它由初始向量和秘密密钥拼接而成。由于初始向量最终与密文序列组合成密文帧,故初始向量是已知的。
假设$K[0],K[1],K[2],……,K[A+2]$是以明文方式传输的IV,秘密密钥为$K[A+3],K[A+4]……$。为了得到$K[A+3]$,可以构造一种特殊格式的$IV(A+3,N-1,x)$,其中 $N$ 为 $S$ 的长度(256), $x$ 为任意值。
下面来跟踪KSA的执行过程。
下图为初始状态$S_{-1}$,此时$i_{-1}=j_{-1}=0$
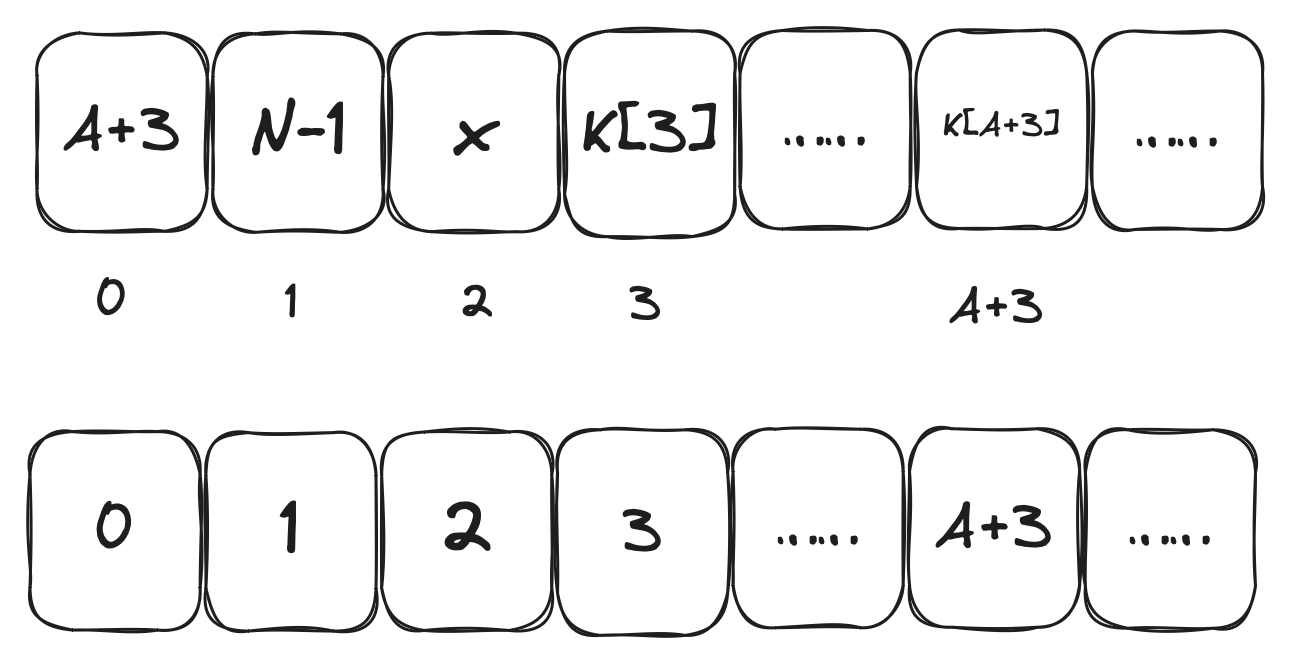
第0步,此时$i_{0}=0$,$j_{0}=j_{-1}+S_{-1}[i_{0}]+K[i_{0}]$,交换$S_{-1}[i_{0}]$与$S_{-1}[j_{0}]$,得到$S_{0}$
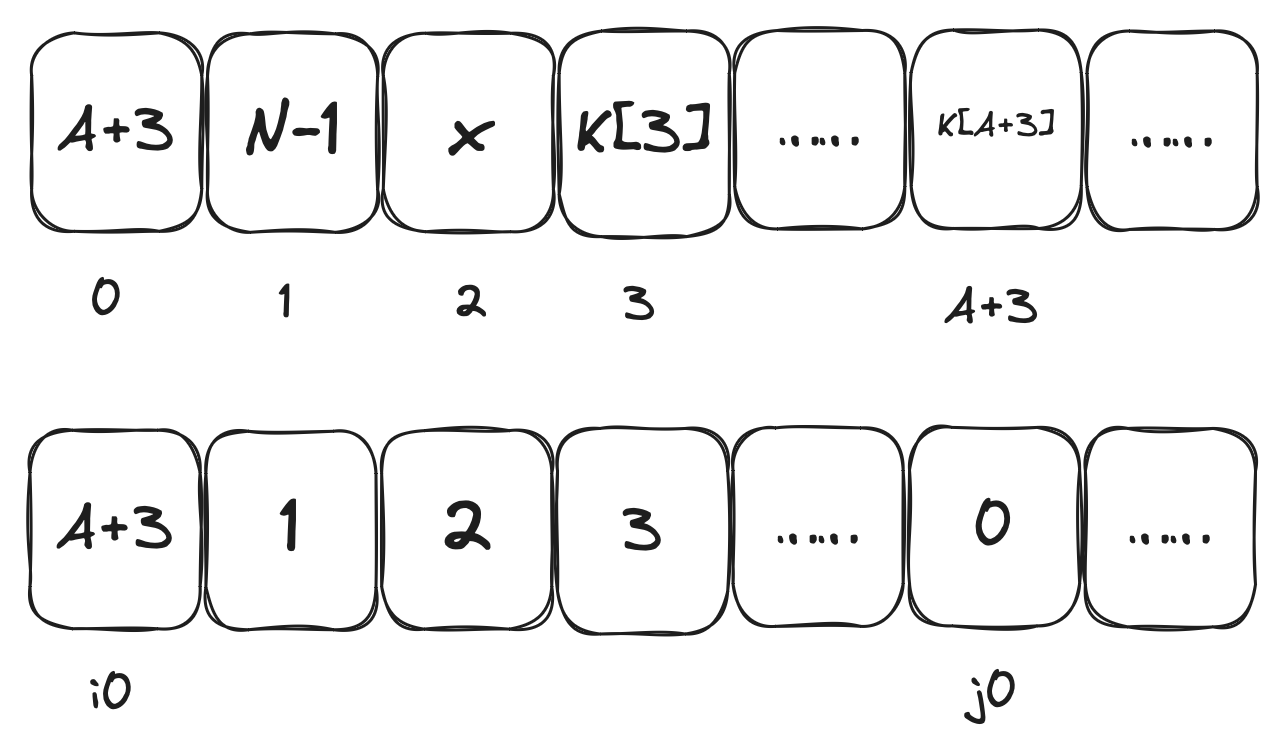
第1步,此时$i_{1}=1$,$j_{1}=j_{0}+S_{0}[i_{1}]+K[i_{1}]=A+3$,交换$S_{0}[i_{1}]$与$S_{0}[j_{1}]$,得到$S_{1}$
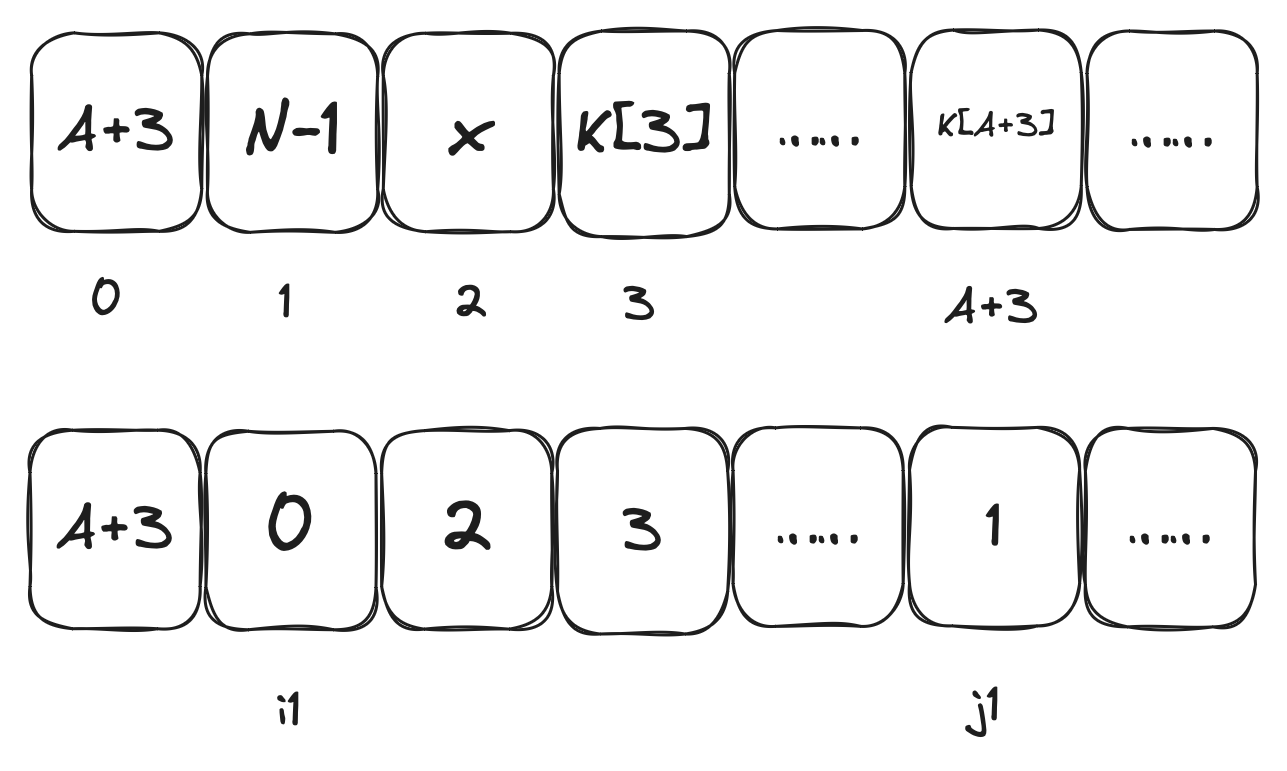
通过观察KSA的步骤可以得知,在A+3轮之前,S的排列与j的值都是可以被计算的。也就是说$S_{A+2}$和$j_{A+2}$是已知的。作为攻击者,使用该法的关键在于,在$S_{A+3}$轮之前必须保证:
$$ S[0]=A+3 $$
$$ S[1]=0 $$
否则应弃用该IV。
第A+3步,此时$i_{A+3}=A+3$,$j_{A+3}=j_{A+2}+S_{A+2}[i_{A+3}]+K[i_{A+3}]$,交换$S_{A+2}[i_{A+3}]$与$S_{A+2}[j_{A+3}]$,得到$S_{A+3}$
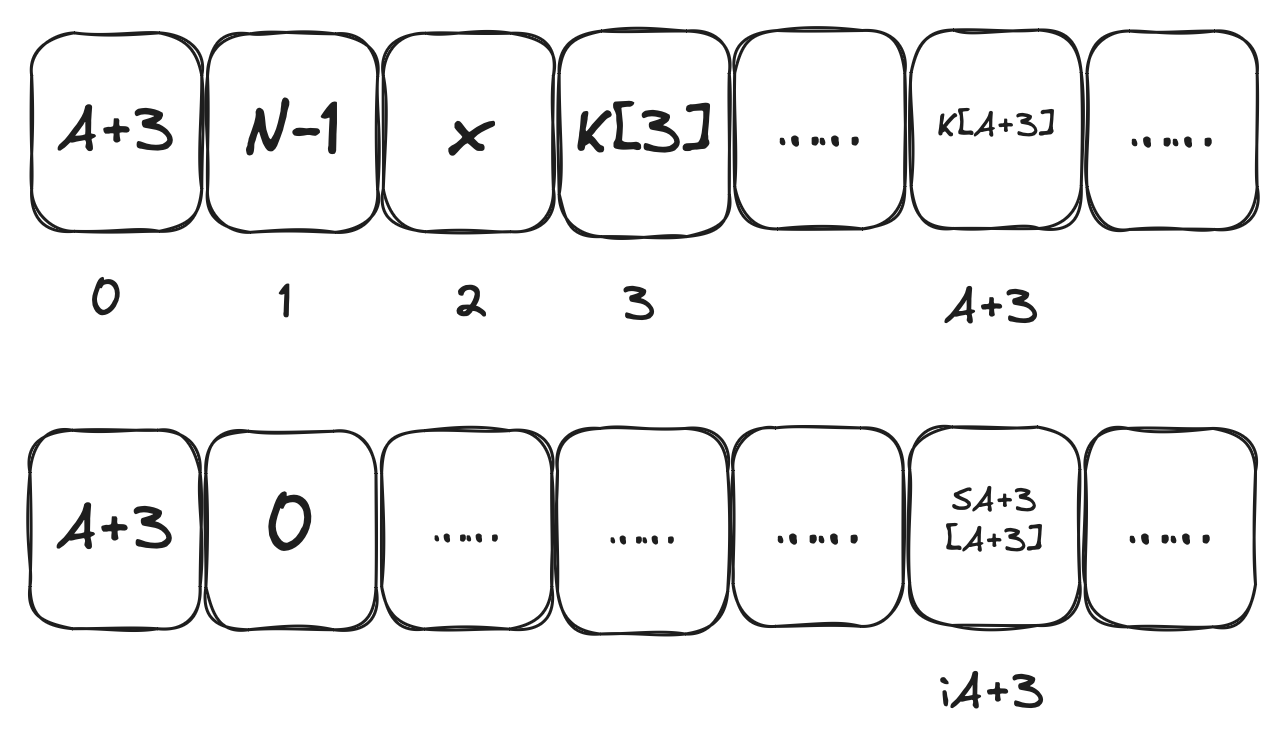
在$S_{A+3}$状态中,令 $X=S_{A+3}[1]=0$,$Y=S_{A+3}[X]=A+3$,则$Z=S_{A+3}[X+Y]=S_{A+3}[A+3]$。有5%的概率,$X$、$Y$、$Z$三个元素都不参与后续的交换,此时PRGA输出的第一个字节为$S_{A+3}[A+3]$。
又因$S_{A+3}[A+3]=S_{A+2}[j_{A+3}]$,由于$S_{A+3}[A+3]=A+3$,只需要找到它在$S_{A+2}$中的位置,即可得知$j_{A+3}$。
由$j_{A+3}=j_{A+2}+S_{A+2}[i_{A+3}]+K[i_{A+3}]$有:
$$ K[A+3]=j_{A+3}-j_{A+2}-S_{A+2}[A+3] $$
使$IV(A+3,N-1,x)$中的 $x$ 取不同值,重复上述步骤即可得到大量的$K[A+3]$估计值,其中出现次数最多的估计值为$K[A+3]$真实值的可能性最大。取其值为$K[A+3]$
,再根据上述步骤类推$K[A+4],K[A+5]……$,直到恢复整个WEP密钥。
FMS攻击揭开了对WEP进行攻击的序幕,此后研究人员又发现了更多令人拍案叫绝的攻击方法,如chop-chop攻击、KoreK攻击、Klein攻击、PTW攻击等,在这些攻击方法的基础上还存在许多改进方法,不过鉴于篇幅(脑力有限),就不一一展开说明了。
如今使用自动化工具(aircrack-ng、wifite等)可以轻松破解WEP,而这些工具就是使用其中的一项或若干项作为原理编写的。
在现实中破解WEP
等手头有设备了再写吧……
后记
其实起初我也只了解过FMS攻击,借着这篇文章的契机才了解到还存在那么多精妙的攻击方法,只得感叹:学海无涯。
计算机技术日新月异,早在2003年,Wi-Fi联盟就主导开发了WPA(Wi-Fi Protected Access),它的目标是提供更强大的加密和认证机制,以解决WEP存在的安全漏洞。
那么,WPA又真的安全吗?
😏